FOR WATER TIGHT STRUCTURES

1. Crack Width Calculation As Per Aci 318 1400
2. Crack Width Calculation As Per Aci 318 14 Pdf
3. Crack Width Calculation As Per Aci 318 14 Free

1. Reasonable crack widths for reinforced concrete under service loads are listed in Table 4.1 of ACI 224R-01. However, a footnote warns that, with time, “a significant portion” of the cracks in a structure can exceed these values. Commentary Provision R24.3.1 of ACI 318-19 discusses flexural reinforcement for one-way slabs and beams.
2. Likely to crack by comparing calculated stresses with the expected concrete strength. The 95 percentile, f 5, should be used to obtain conservative values for restraint forces that might occur before the concrete cracks. These restraint forces are used to calculate the amount of reinforcement needed for crack width control. Causes of Cracking.
3. Calculate the required reinforcement to resist the moment at the stem base: Mu t Use #8 bars with 2.0 in. Concrete cover per ACI 318-14 (Table 20.6.1.3.1). The distance from extreme compression fiber to the centroid of longitudinal tension reinforcement, d, is calculated below: d.

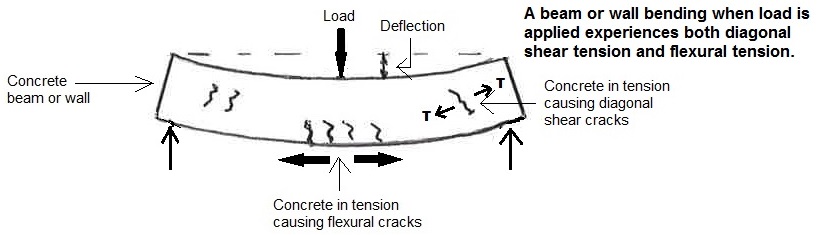
4.3—Crack control in two-way slabs and plates 4.4—Tolerable crack widths versus exposure conditions in reinforced concrete 4.5—Flexural cracking in prestressed concrete 4.6—Anchorage-zone cracking in prestressed concrete 4.7—Crack control in deep beams 4.8—Tension cracking Reported by ACI.

Crack width is a complex and tough topic. Most people still use 20 years old method defined in ACI 318-95. The situation becomes more complex if axial tension force and moment is combined to calculate crack width. One of the examples is large water tanks above ground. This tutorial aims at explaining details and methods in different ACI documents. Latest method defined in ACI 350-06 should be used. Given the variability and non-linear behaviour in long-term deflection and crack widths, it is NOT NEEDED to go for detailed sophisticated calculations for these effects. You can imagine this as calculating something non-linear (crack widths or long-term deflection) from linear-elastic analysis. You have to have some approximations for that. No matter how detailed are your calculations, you still can’t predict for certain the long-term deflection and crack widths.

Three ACI documents for crack width; ACI 224R-01, ACI 350-01 & ACI 350-06

1. ACI 224R-01

Some notes:-

• Table 4.1 is based on Nawy findings.
• The table is just a general guide line.
• The table gives w=0.004″ or 0.10mm for water retaining structures.
• It is expected that portion of cracks will exceed these values by a significant amount.
• No relationship between level of cracking & corrosion in long-term.
• More cover can be used even if it yields larger crack width, against corrosion.
• ACI methods deal only with conventional concrete for crack width.
• Crack width is directly proportional to dia of bar & fs and inversely to area of steel.
• Three reasons for limiting crack widths
  1-Appearance
  2-Corrosion
  3-Water tightness

There are three methods mentioned in this document

A) ACI 318-95

Statistical method of Gergely & Lutz 1968

Covers up to 2.5″ only

Crack Width Calculation As Per Aci 318 1400

z in any units

For two-way slabs see section 4.3 of ACI 224R-01

For shallow beams/thick one-way slabs: (w in inches)

Thick means L/D = 15-20

d used here will be distance to the center of bottom bar nearest to tension face.

ß=1.25 to 1.35 if cc≥1″

ACI 318-95 section 10.6 says use ß=1.20 & fs=0.6fy

ACI 340R has design aids for z

ACI 318-98 & earlier max z=175 kip/in for interior exposure based on 0.41mm probable crack width(0.016″)

ACI 318 max z=145 kip/in for exterior exposure based on 0.33mm probable crack width(0.013″)

B) ACI 318-99

No distinction for interior/exterior exposure

For beams & one-way slabs:

fs=0.6fy

Not for aggressive/water tight structures

C) EUROPEAN CODES

—————————————————————————————————————————

2. ACI 350-01

Same concept like ACI 224R-01

—————————————————————————————————————————

3. ACI 350-06

2 types of exposure:-

i)Normal

ii)Severe

can be taken = 25

where c is at service load

ß can be taken = 1.20 for h≥16″

& 1.35 for h<16″

where appearance is of concern & cover exceeds 3″, also check equation 10-7

Exposure defined as

Previous codes (ACI 350-01) puts following limits on z:

Normal exposure: z=115 kip/in (w=0.010″ or 0.254mm)

Severe exposure: z= 95 kip/in (w=0.009″ or 0.229mm)

—————————————————————————————————————————

EXAMPLE WITH AXIAL TENSILE LOAD AND MOMENT

• For detailed calculations, find the N.A. depth but use ԑ at service loads. Strain diagram will be different from the one shown in figure above if axial load is included.
• Assume no strength from concrete due to axial tension load.
• Assume tension force acting at steel reinforcement level.
• Assume all the moment is resisted by top and bottom steel only.
• Tension at top steel; T1 = A’s / (A’s+As+As1+As1) x Total Tension Force
• Tension at bottom steel;T2 = As / (A’s+As+As1+As1) x Total Tension Force
• Tension at right steel; T3 = As1/ (A’s+As+As1+As1) x Total Tension Force
• Tension at left steel; T4 = As1/ (A’s+As+As1+As1 )x Total Tension Force

• Taking moment about top steel:

M=Asfs(d-d’)+T2(d-d’)+0.5T3(h/4)+0.5T4(h/4)

T3=T4 so

M=Asfs(d-d’)+T2(d-d’)+T3(h/4)

(where T is total axial tension force)

From here calculate fs and compare with fsmax of ACI 350-06.

Eurocode 2 part 1-1: Design of concrete structures 7.3 Crack control

The crack width, w_k, may be calculated as follows:

wk = sr,max⋅(εsm - εcm)

(7.8)

where:

s_r,max

is the maximum crack spacing

ε_sm

is the mean strain in the reinforcement under the relevant combination of loads, including the effect of imposed deformations and taking into account the effects of tension stiffening

ε_cm

is the mean strain in the concrete between cracks.

(7.9)

where:

σ_s

is the stress in the tension reinforcement assuming a cracked section,
see application for a rectangular section or application for a T-section

E_s

is the design value of the modulus of elasticity of the reinforcing steel, see § 3.2.7 (4)

α_e

is the ratio E_s/E_cm

with

E_cm

the secant modulus of elasticity of concrete

f_ct,eff

is the mean value of the tensile strength of the concrete effective at the time when the cracks may first be expected to occur:
f_ct,eff = f_ctm or lower, (f_ctm(t)), if cracking is expected earlier than 28 days

ρ_p,eff

= (As + ξ1⋅A'p)/Ac,eff

(7.10)

with

A_s

the cross sectional area of reinforcement

A'_p

the area of pre or post-tensioned tendons within A_c,eff

A_c,eff

the effective area of concrete in tension surrounding the reinforcement or prestressing tendons of depth, h_c,ef, where h_c,ef is the lesser of 2,5(h - d), (h - x)/3 or h/2 (see Figure 7.1)

ξ₁

the adjusted ratio of bond strength taking into account the different diameters of prestressing and reinforcing steel:

ξ1 =

(7.5)

with

ξ

the ratio of bond strength of prestressing and reinforcing steel, according to Table 6.2

Φ_S

the largest bar diameter of the reinforcing steel

Φ_P

the diameter or equivalent diameter of prestressing steel:
Φ_p = 1,6⋅√A_P for bundles, where A_P is the area of a prestressing steel,
Φ_p = 1,75⋅Φ_wire for single 7 wire strands,
Φ_p = 1,20⋅Φ_wire for single 3 wire strands, where Φ_wire is the wire diameter.

k_t

is a factor dependent on the duration of the load:
k_t = 0,6 for short term loading,
k_t = 0,4 for long term loading.

• Where the bonded reinforcenlent is fixed at reasonably close centres within the tension zone (spacing ≤ 5(c + Φ/2), cf. Figure 7.2), the maximum crack spacing s_r,max may be calculated as follows:

sr,max = k3c + k1k2k4Φ / ρp,eff

(7.11)

where:

Φ

is the bar diameter. Where a mixture of bar diameters is used in a section, an equivalent diameter, Φ_eq, should be used.

c

is the cover to the longitudinal reinforcement

ρ_p,eff

see the difference of the mean strains above

k₁

is a coefficient which takes account of the bond properties of the bonded reinforcement:
k₁ = 0,8 for high bond bars,
k₁ = 1,6 for bars with an effectively plain surface (e.g. prestressing tendons).

k₂

is a coefficient which takes account of the distribution of strain:
k₂ = 0,5 for bending,
k₂ = 1,0 for pure tension.
Intermediate values of k₂ should be used for cases of eccentric tension or for local areas:

k2 = (ε1 + ε2)/(2ε1)

(7.13)

where ε₁ is the greater and ε₂ is the lesser tensile strain at the boundaries of the section considered, assessed on the basis of a cracked section.

k₃

is a Nationally Determined Parameter, see § 7.3.4 (3)

k₄

is a Nationally Determined Parameter, see § 7.3.4 (3).

Crack Width Calculation As Per Aci 318 14 Pdf

• Where the spacing of the bonded reinforcement exceeds 5(c + Φ/2) (cf. Figure 7.2), or where there is no bonded reinforcement within the tension zone, the maximum crack spacing s_r,max may be calculated as follows:

sr,max = 1,3(h - x)

(7.14)

where:

h

is the overall depth of the section (see Figure 7.1)

x

is the neutral axis depth of the section (see Figure 7.1).

This application calculates the crack width w_k from your inputs. Intermediate results will also be given.

First, change the following option if necessary:

Output

Crack Width Calculation As Per Aci 318 14 Free